树上差分

简单高效地实现树上区间修改操作。

步骤

1. 首先先建立一个辅助数组，使用 $fa[k][i]$ 表示 $i$ 的 $2^{k}$ 级祖先，随后 dfs 一遍求出该数组。
2. 实现求 $lca$ 的函数。
   具体实现：
   1. 已知两点 $u, v$ ，我们不妨令 $u$ 是其中深度较大的那位；
   2. 提升 $u$ 的高度，直至其高度等于 $v$ 的高度；
   3. 「检查」如果此时我们发现 $u = v$ ，那么此时 $u, v$ 的 $lca$ 就是 $u$。
   4. 「否则」我们从 $2^{k}(k = 31 \to 0)$ 找起，依次判断 $fa[k][u]$ 是否等于 $fa[k][v]$，若不等则将两个节点向上提。此时最多遍历 $31$ 次。

不妨假设我们从 $u$ 到 $v$ 的路径都添加数值 $x$ ，那么显然我们只需要将 $u \to v$ 这段路径拆成 $u \to lca$ 和 $lca \to v$ 。

又因为我们使用 dfs 回溯来求点上值，于是我们会自然而然地想到，$val[u] \leftarrow val[u] + x$ 和 $val[v] \leftarrow val[v] + x$。

考虑贡献。由于在回溯时 $lca$ 的点权会被多计算一次，因此减去 $x$。并且有 $fa[0][lca]$ ，即 $lca$ 的父亲也会被删除一次，如图：

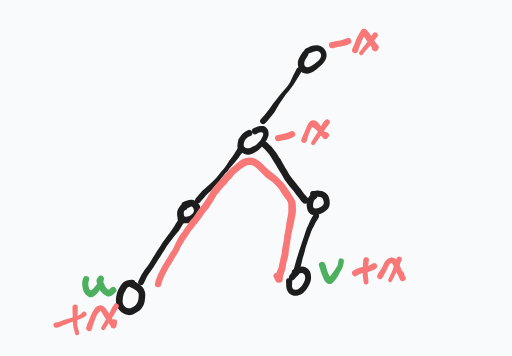
所以有：

vl[u] += x;
vl[v] += x;
vl[lca(u,v)] -= x;
vl[fa[0][lca(u,v)] -= x;

注意事项

以上讨论的是点差分。对于边差分，我们可以将边绑定到 深度较高 的节点上，然后稍微修改一下赋值逻辑，其他同理：

vl[u] += x;
vl[v] += x;
vl[lca(u,v)] -= 2*x;

优化

摘自 OI-Wiki | 最近公共祖先：
倍增算法的预处理时间复杂度为 $O(n\log n)$，单次查询时间复杂度为 $O(\log n)$。 另外倍增算法可以通过交换 fa 数组的两维使较小维放在前面。这样可以减少 cache miss 次数，提高程序效率。

关联题

洛谷 P3128 - # [USACO15DEC] Max Flow P